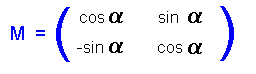
Frequently Asked mathematical Questions ('FAQs')
Question1: What is a fractal ?
Question2: What is a Lissajous oscillation ?
Answers: look below for 2 examples
(click with mouse to zoom in ; press keys 'b' or 'c' to reset view or iteration sequence
use key 'L' or 'l' to switch to Lissajous display)
Question: How can i derive a fractional polynome P(x)/Q(x) ?
Answer: with the formula q' = (f/g)' = (f'g-fg') / g2
example:
| q =
|
2x2 + x
--------
x3+2x2
|
with:
f'g = (4x+1) * (x3+2x2) = 4x4+9x3+2x2
fg' = (2x2 + x) * (3x2+4x) = 6x4+11x3+4x2
...
Question: Why is the derivation of
a) sin(x) = cos(x) ?
b) x2 = 2*x ?
Question: What is a 'Matrix' ?
Answer: n*m numbers or mathematical terms grouped in n different lines
note: the software developpers of the special-effects crew of the movie "THE MATRIX" had to
use 'rotational matrices' to generate some of the 3D computergraphic effects:
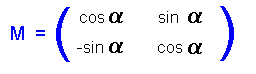
rotated coordinates : v' = M * v
(v = vector {x,y} with old point-coordinates)
Question: What is Pascal's Triangle ?
Answer: The numbers on each line of P.T. are generated by summing the 2
neighbours on the previous line above.
The first and last boundary number always is 1.
(click on arrows or use number keys '1' or '2' to go through the several ways of formula usage)
sourcecode of a P.T. matrix generator for a programmable Casio pocket calculator:
| Prog1: |
"Matrix n over k ; Pascals Triangle":Prog 2:Mat Ans->Mat A
:10->N:Lbl 0:N->K:Lbl 1:(N-1)|C(K-1)->Mat[N,K]:Dsz K:Goto 1:
Dsz N:Goto 0:Mat A
| | Prog2: |
'10*10 Matrix set auxiliary program':[[0,0,0,0,0,0,0,0,0,0]]:
(Trn Mat Ans)*(Mat Ans)
|
notes:
start Prog1 to see the result
the " |C " sign can be reached via the "Math->Prb->nCr" menu sequence
(key sequence "Shift-5 , F2 , F3" on a "Casio CFX-9800G" calculator).
Physics
Mach Angle alpha for supersonic flight of an object with velocity v in a medium with a speed of sound c :
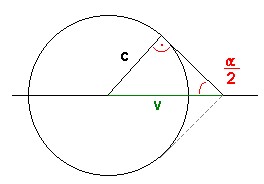
sin (alpha/2) = c/v = 1/M
( M = Mach number ; e.g. M=2 for v = twice the speed of sound )
Question: When does y(t) = Y0 * e(-k*t) reach half of its initial value Y0 ?
Answer:
0.5 * Y0 = Y0 * e(-k*t) | : Y0 (allowed for Y0<>0)
0.5 = e(-k*t) | ln
ln 0.5 = -k*t | : (-k)
-ln 0.5
------- = t
Q: After how many oscillations (n) does the amplitude of
an oscillation of type y(t) = Y * sin(omega * t) * e(-k*n*T)
reach 10% of its initial value (Y) ?
A:
0.1 * Y = Y * e(-k*n*T) | :Y (allowed for Y<>0)
0.1 = e(-k*n*T) | ln
ln 0.1 = -k*n*T | : (-k*T)
-ln 0.1
------- = n
with e.g. k=0,046 s^-1 and T = 1,83 s
=> n = 27 oscillations
Q: What is the velocity function v(t) of an oscillation of type y(t) = Y * cos(omega * t) * e(-k*t) ?
A:
v(t) = (dy/dt) y(t) = y'(t) = Y * [ cos(omega * t) * e(-k*t) ]'
= Y * [ cos(omega * t)' * e(-k*t) + cos(omega * t) * (e(-k*t))' ]
= Y * [ -omega*sin(omega * t) * e(-k*t) + cos(omega * t) * (-k) * e(-k*t) ]
= Y * [ -omega*sin(omega * t) * e(-k*t) - cos(omega * t) * k * e(-k*t) ]
= Y * e(-k*t) * [ -omega * sin(omega * t) - k * cos(omega * t) ]
(this page has been updated on February-21-2007)
|